Parabolas
Focus

A fixed point F (0 , f) and the straight line y = -f have been given.
P is any point and V is its projection at that line.
P(x , y) is chosen so, that FP = PV. It can be done in infinite ways.
What is the shape of the collections of points P, so what is the locus of P?
FP = √{(x-0)2 + (y-f)2} and PV = y+f
So x2 + (y-f)2 = (y + f)2 or y = x2/(4f)
It is a parabola with its minimum in (0 , 0).
In the math lesson is told, that such a parabola is presented by y = ax2.
Obviously a = 1/(4f) or f = 1/(4a) or 4af = 1.
The given line is called the directrix of the parabola.
F is called the focus and f the focal length being the distance from F to the top.
Any shift of the parabola leads to the equation y = ax2 + bx + c or
y = x2 /(4f) + bx + c
Parabolic mirror
A parallel beam of light falling on a parabolic mirror is reflected to a
point F’on a line perpendicular to the axis of the parabola.
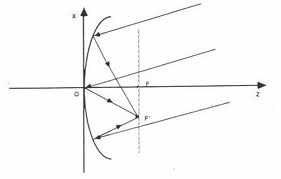
The light beam through F is reflected parallel to the main axis.
This way you find F’.
De parabola star
The parabola y = (1/8)x2 + 2 meets the points (-4 , 4) and (4 , 4).
The top is at (0 , 2) and F at (0 , 4 ), because f = 2.
The tangent at (4 , 4) is the line y = x. The tangent at (-4 , 4) is the line y = -x.
Please, check it yourself.
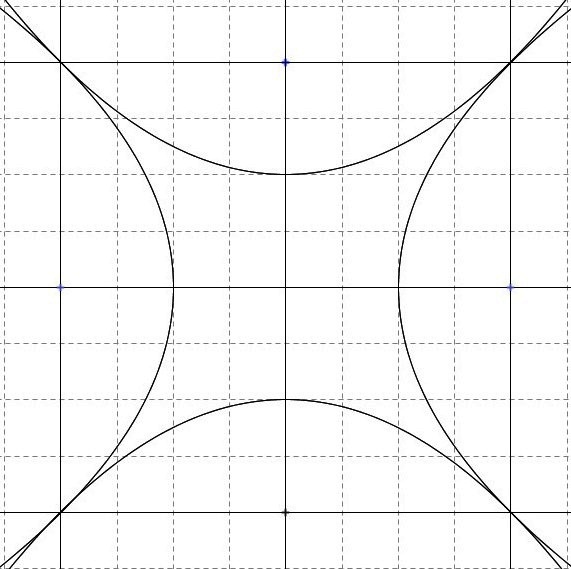
Design the mirror image of this parabola relative to the x-axis.
Design the mirror image of this parabola relative to y = x.
Design the mirror image of this parabola relative to y= -x.
Then a ‘parabola star’ arises.
The adjoining parabolas touch each other at the vertices.
Similarity
If a is tall and so f is small, then the parabola is narrow and like a bullet.
If a is small and so f is tall, then the parabola wide as an umbrella.
But still: all parabolas are similar.
Check the top of the 'pointy' parabola with a magnifying glass.
| parabola | vergelijking | f |
| 1 | 3x2 | 1/12 |
| 2 | (1/5)x2 | 5/4 |
The f of parabola 2 is 15 × so tall as the f of parabola 1.
The (linear) magnification factor is 15.
All lengths in parabola 2 are 15 × the corresponding lengths in parabola 1.
Parabolic wave
Consider the ↑ parabola y= -px(x-2a) from x=0 up to and including x=2a.
The maximum is (a , pa2).
Find a new parabola by rotating this ↑ parabola 180° around point (2a , 0).
Then you get a congruent ↓ parabola which reaches from x=2a up to and including x=4a.
The minimum is ( 3a , -ap2).
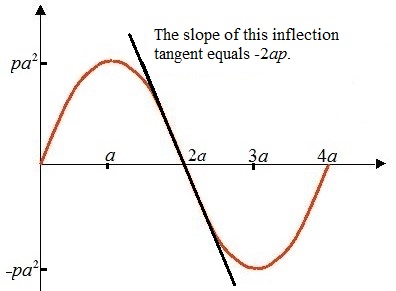
A complete 'wavelength' with length 4a arises.
This figure may be extended with as much congruent wavelength as wanted,
to the left and to the right.
The wave does not show any gap or jump, in particular at the points of intersection with the x-axis.
We ourselves made the wave continuous.
It can be shown by differential calculus, that the wave has not a kink at x = 2a
nor at any point 4a further along the x-axis.
The derivative of y= -px(x-2a) = -px2 + 2apx is y’= -2px + 2ap.
If x = 2a, then y’ = -2p.2a + 2ap = -2ap.
So the slope of the ↑ parabola at x=2a is -2ap.
Likewise, it can be understood that the steepness of the ↓ parabola at x=2a equals -2ap as well.
It means that the two parabolas have a common tangent.
This line is an inflection tangent to the wave.
The wave is differentiable at any point, especially at x = 0 + k.2a.
The parabola wave does not shows any kink.
If one would draw a sine wave with the same wavelength 4a and the same amplitudo pa2
in the same coordinate system, then a difference relative to the parabolic wave is hardly seen.



