cos18°
During lessons about goniometry is explained how to calculate
the sine, cosine and tangent of 30°, 45° and 60°.
Can an exact calculation be done for other angles?
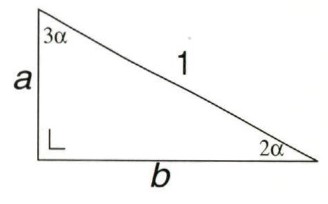
In the trangle below it is easily seen that 5α equals 90°.
Then α = 18°, 2α = 36° and 3α = 54°.
cos3α
From goniometry it is known, that cos3α = 4cos3α - 3cosα.
You can find the proot below. You may skip it.You can see from the figure:The proof of cos3α = 4cos2 α - 3cosα
A standard formula from trigonometry is
cos(α + β) = cosαcosβ – sinαsinβ.
Choose β = 2α. Then
cos(α + 2α) = cosαcos2α – sinαsin2α
cos3α =
cosα(2cos2α - 1) - sinα(2sinαcosα) =
cosα{(2cos2α - 1) - 2sin2α} =
cosα{(2cos2α - 1) - 2(1 - cos2α)}
So cos3α = 4cos3α - 3cosα.cos3α = a/1. It is proven, that cos3α = 4cos3α - 3cosα.Here the Pythagorean theorem gives a2 + b2 = 1.
So a = 4cos3α - 3cosα. This is equation (1).
cos2α = b/1. It is known, that cos2α = 2cos2α - 1,
So b = 2cos2α - 1. This is equation (2).
Combinee it with equations (1) and (2):
(4cos3α - 3cosα)2 + (2cos2α - 1)2 = 1
Temporarily change cosα into p.
(4p3 - 3p)2 + (2p2 - 1)2 = 1
(16p6 - 24p4 + 9p2) + (4p4 - 4p2 + 1) = 1
16p6 - 20p4 + 5p2 = 0 of p2(16p4 - 20p2 + 5) = 0.
p = 0 does not satisfy, so 16p4 - 20p2 + 5 = 0.
Temporarily change p2 into x. Because 0 ≤ cosα ≤ 1, also 0 ≤ p ≤ 1 is true.
16x2 - 20x + 5 = 0. It gives x = {5 + √5)/8.
p2 = x = (5 ± √5)/8 and p = cos18°, so p = √{(5 ± √5)/8}.
p2 = 0·9510565 or p = 0·5877852. According to my pocket calculator cos18° equals 0.9510565.
Apparently the exact description is: cos18° = √(5+√5)/8.
By means of the earlier mentioned formula cos2α = 2cos2α - 1 it is possible to find
an exact expression for cos36° and cos72°. Even for cos9°.
With cos3α = 4cos2α - 3cosα we find an exact expression for cos54°.
With cos54° = 2cos227° – 1 we conjure up cos27°.
Sine
An exact expression of the sine of every mentioned angle can be found with cosα = sin(90° - α).
Tangent
An exact expression of the tangent of every mentioned angle can be found with tanα = sinα / cosα.
Look at the goniometrical table.
Another triangle
Using a triangle with angels α, 4α en 90° gives a similar result.
Multiples of 9°
With sin(α ± β) = sinαcosβ ± cosαsinβ and
cos(α + β) = cosαcosβ + sinαsinβ
all angels being a multiple of 9° can be found.
Exact goniometrical table Menu math Sciences