Hele getallen voorbeelden
2 Stambreuken optellen
3 Stambreuken optellen
Gemiddelden, delers en veelvouden
Pythagoras 1
Pythagoras 2
Kwadraatslierten
Middelbare waarde; twee termen
Middelbare waarde; drie termen
Middelbare waarde; meertermen
Pythagoras driedimensionaal
Pythagoras meerdimensionaal
Kwadratische stambreuken
De oppervlakte van driehoeken
Zes ribben en vier oppervlakken van een driezijdige piramide
Willekeurig viervlak; drie verschillende oppervlakken
Willekeurig viervlak; twee verschillende oppervlakken
Willekeurig viervlak; gelijke oppervlakken
2 Stambreuken optellen
Stambreuken zijn bruikbaar bij de lenzenformule en bij de berekening van
een substitutieweerstand van twee parallel geschakelde weerstanden.
Als 1/a + 1/b = 1/c dan is ook 1/(ak) + 1/(bk) = 1/(ck).
Stambreuken 1/{n(m+n)} + 1/{m(m+n)} = 1/{mn} 1/2 + 1/2 = 1/1 1/3 + 1/6 = 1/2 1/4 + 1/12 = 1/3 1/14 + 1/35 = 1/10 1/18 + 1/63 = 1/14 1/21 + 1/28 = 1/12 1/24 + 1/40 = 1/15 1/30 + 1/70 = 1/21 1/36 + 1/45 = 1/20 1/44 + 1/77 = 1/28 1/52 + 1/117 = 1/36 1/55 + 1/66 = 1/30 1/60 + 1/84 = 1/35 1/65 + 1/104 = 1/40 1/78 + 1/91 = 1/42 1/102 + 1/187 = 1/66 1/114 + 1/247 = 1/78 1/105 + 1/120 = 1/56 1/112 + 1/144 = 1/63 1/119 + 1/170 = 1/70 1/136 + 1/153 = 1/72 1/152 + 1/209 = 1/88
Omhoog
3 Stambreuken optellen
Drie parallelle weerstanden Drie parallelle weerstanden 1/2 + 1/3 + 1/6 = 1/1 1/3 + 1/3 + 1/3 = 1/1 1/18 + 1/35 + 1/63 = 1/10 1/28 + 1/30 + 1/70 = 1/12 1/30 + 1/119 + 1/170 = 1/21 1/55 + 1/66 + 1/70 = 1/21 1/56 + 1/40 + 1/42 = 1/15 1/60 + 1/156 + 1/182 = 1/35 1/91 + 1/114 + 1/247 = 1/42 1/152 + 1/154 + 1/209 = 1/56
Omhoog
Gemiddelden, delers en veelvouden
g = g(a,b) = grootste gemeenschappelijke deler van a en b
h = h(a,b) = het harmonische gemiddelde van a en b. Hierin is 1/a + 1/b = 1/h + 1/h.
m = m(a,b) = meetkundig gemiddelde van a en b. Hierin is ab = m2
r = r(a,b) = rekenkundig gemiddelde van a en b. Hierin is a + b = r + r
k = k(a,b) = kleinste gemeenschappelijke veelvoud van a en b
Weet, dat gk = ab = hr = m2 en g ≤ a < h < m < r < b ≤ k.
Gehele getallen:
x y g a h m r b k x y g x2g x2y2 xyg g2 y2g x2y2g 1 3 5 5 9 15 25 45 45 10 10 16 20 25 40 40 1 5 13 13 25 65 169 325 325 3 5 17 153 225 255 289 425 3825 1 7 25 25 49 175 625 1225 1225 3 7 29 261 441 609 841 1421 12789 5 7 37 925 1225 1295 1369 1813 45325 1 9 41 41 81 369 1681 3321 3321 3 9 45 405 729 1215 2025 3645 32805 5 9 53 1325 2025 2385 28095 4293 10732 7 9 65 3185 3969 4095 4225 5265 257985 1 11 61 61 121 671 3721 7381 7381 3 11 65 585 1089 2145 4225 7865 70785 5 11 73 1825 3025 4015 5329 8833 220825 7 11 85 4165 5929 6545 7225 10285 503965 9 11 101 8181 9801 9999 10201 12221 989901
Omhoog
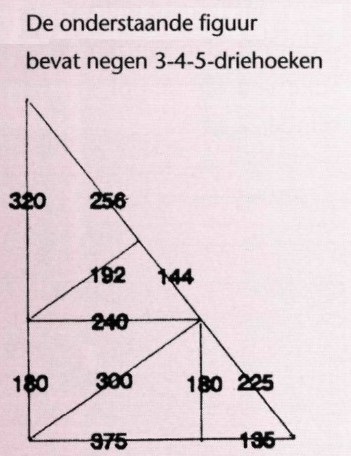
Pythagoras 1
Als a2 + b2 = c2 is, is ook (ap)2 + (bp)2 = (cp)2
{2mn}2 + {m2– n2}2 = {m2 + n2}2 {2mn}2 + {m2– n2}2 = {m2 + n2}2 {2mn}2 + {m2– n2}2 = {m2 + n2}2 32 + 42 = 52 52 + 122 = 132 72 + 242 = 252 202 + 212 = 292 82 + 152 = 172 122 + 352 = 372 282 + 452 = 532 482 + 552 = 732 162 + 632 = 652 92 + 402 = 412 332 + 562 = 652 652 + 722 = 972 112 + 602 = 612 392 +802 = 892 962 + 1102 = 1462 132 +842 = 852 852 + 1322 = 1572 1332 + 1562 = 2052 152 + 1122 = 1132 362 + 772 = 852 202 + 992 = 1012 602 + 912 = 1092 512 + 1402 = 1492 192 + 1802 = 1812 222 + 1202 = 1222 442 + 1172 = 1252 882 + 1052 = 1372 852 + 1322 = 1572 572 + 1762 = 1852 212 + 2202 = 2212 1192 + 1202 = 1692 952 + 1682 = 1932 232 + 2642 = 2652 522 + 1652 = 1732 1042 + 1532 = 1852 102 + 2082 = 2332
Omhoog
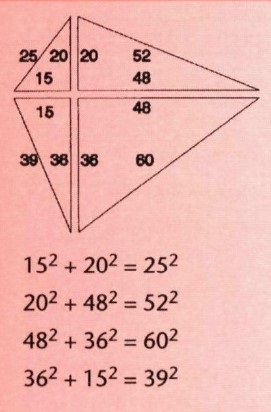
Pythagoras 2
12 + 82 = 42 + 72.
72 + 242 = 152 + 202 = 252.
132 + 842 = 362 + 772 = 852.
162 + 632 = 252 + 602 = 652.
Kwadraatslierten
De som van de eerste 24 kwadraten is 702.
De som van de eerste 963 kwadraten is 172672.
De som van de eerste 994 kwadraten is 181072.
De som van de eerste 1053 kwadraten is 197422.
De som van de eerste 1199 kwadraten is 239852.
De som van de eerste 1200 kwadraten is 240152.
De som van de eerste 1329 kwadraten is 279882.
De som van de eerste 1727 kwadraten is 414542.
De som van de eerste 1728 kwadraten is 414902.
De som van de eerste n kwadraten is n(n+1)(2n+1)/6.
De som van de eerste 10 getallen = de som van de eerste 5 kwadraten = 55.
De som van de eerste 13 getallen = de som van de eerste 6 kwadraten = 91.
De som van de eerste 645 getallen = de som van de eerste 85 kwadraten = 208335.
22 + 42 + 62 + ... + 462 + 482 = 1402.
Vermoeden: de som van de eerste n oneven kwadraten is geen kwadraat.
Onderzocht tot als de laatste term 9999 is.
22 + 52 + 82 + ... + 232 + 262 = 482.
Omhoog
Middelbare waarde; twee termen
Als a2 + b2 = c2, dan is (a – b)2 + (a + b)2 = c2 + c2.
c is de middelbare waarde van a-b en a+b.
Twee termen Twee termen 12 + 72 = 52 + 52 792 + 1192 = 1012+ 1012 72 + 172 = 132 + 132 312 + 1512 = 1092 + 1092 72 + 232 = 172 + 172 972 + 1272 = 1132 + 1132 172 + 312 = 252 + 252 1272 + 1612 = 1452 + 1452 122 + 412 = 292 + 292 1192 + 1672 = 1452 + 1452 232 + 472 = 372 + 372 892 + 1912 = 1492 + 1492 312 + 492 = 412 + 412 12 + 2392 = 1692 + 1692 172 + 732 = 532 + 532 1612+ 1992 = 1812 + 1812 492 + 712 = 612 + 612 732 + 2632 = 19322 + 1932 232 + 892 = 652 + 652 1582 + 2382 = 2022 + 2022 472 + 792 = 652 + 652 1132 + 2172 = 1732 +1732 72 + 1032 = 732 + 732 492 + 2572 = 18522 + 1852 712 + 972 = 852 + 852 232 + 2892 = 2052 + 2052 412 + 1132 = 852 + 852 1032 + 3132 = 2332 + 2332 412 + 1192 = 892 + 892 1912 + 3292 = 2692 + 2692 72 + 1372 = 9722 + 972 2382 + 3342 = 2902 + 2902
Middelbare waarde; drie termen
52 + 132 + 132 = 112 + 112 + 1122 52 + 72 + 132 = 92 + 92 + 92 22 + 22 + 102 = 62 + 62 + 62 52 + 72 + 172 = 112 + 112 + 112 52 + 112 + 192 = 132 + 132 + 132 112 + 112 + 252 = 172 + 172 + 172 132 + 132 + 232 = 172 + 172 + 172 132 + 172 + 252 = 192 + 192 + 192 132 + 232 + 252 = 212 + 212 + 212
Middelbare waarde; meertermen
12 + 32 + 32 + 92 = 52 + 52 + 52 + 52 22 + 42 + 42 + 82 = 52 + 52 + 52 + 52 32 + 52 + 92 + 92 = 72 + 72 + 72 + 72 32 + 32 + 32 + 132 = 72 + 72 + 72 + 72 32 + 52 + 92 + 92 = 72 + 72 + 72 + 72 42 + 42 + 82 + 102 = 72 + 72 + 72 + 72 52 + 52 + 52 + 112 = 72 + 72 + 72 + 72 12 + 32 + 52 + 172 = 92 + 92 + 92 + 92 12 + 72 + 72 + 152 = 92 + 92 + 92 + 92 32 + 52 + 112 + 132 = 92 + 92 + 92 + 92 42 + 82 + 102 + 122 = 92 + 92 + 92 + 92 82 + 82 + 102 + 162 = 112 + 112 + 112 + 112 52 + 52 + 72 + 152 = 92 + 92 + 92 + 92 92 + 92 + 152 + 172 = 132 + 132 + 132 + 132 92 + 132 + 172 + 192 = 152 + 152 + 152 + 152 32 + 52 + 52 + 292 = 152 + 152 + 152 + 152 102 + 122 + 162 + 202 = 152 + 152 + 152 + 152 112 + 132 + 132 + 212 = 152 + 152 + 152 + 152 102 + 162 + 202 + 202 = 172 + 172 + 172 + 172 112 + 132 + 232 + 252 = 192 + 192 + 192 + 192 122 + 182 + 202 + 242 = 192 + 192 + 192 + 192 112 + 172 + 252 + 272 = 212 + 212 + 212 + 212 162 + 162 + 162 + 262 = 192 + 192 + 192 + 192 152 + 172 + 252 + 252 = 212 + 212 + 212 + 212
Omhoog
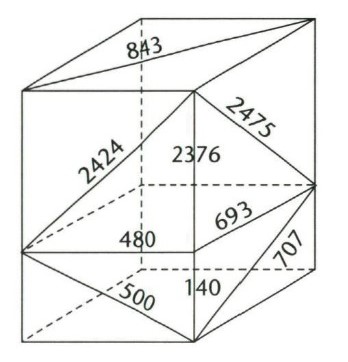
Pythagoras driedimensionaal
De lichaamsdiagonaal van een balk
Als a2 + b2 + c2 = d2 is, is ook (ap)2 + (bp)2 + (cp)2 = (dp)2
22 + 32 + 62 = 72 12 + 42 + 82 = 92 22 + 62 + 92 = 112 32 + 42 + 122 = 132 22 + 52 + 142 = 152 22 + 102 + 112 = 152 82 + 92 + 122 = 172 12 + 62 + 182 = 192 62 + 102 + 152 = 192 42 + 52 + 202 = 212 42 + 82 + 192 = 212 42 + 132 + 162 = 212 82 + 112 + 162 = 212 32 + 62 + 222 = 232 62 + 132 + 1822 = 232 122 + 152 + 162 = 252 22 + 72 + 262 = 272 22 + 102 + 252 = 272 32 + 122 + 242 = 272 72 + 142 + 222 = 272 122 + 162 + 212 = 292 112 + 122 + 242 = 292 52 + 62 + 302 = 312 62 + 142 + 272 = 312 12 + 82 + 322 = 332 42 + 72 + 322 = 332 32 + 82 + 362 = 372 62 + 102 + 332 = 352 92 + 242 + 322 = 412 102 + 142 + 352 = 392 22 + 92 + 422 = 432 62 + 72 + 422 = 432 12 + 102 + 502 = 512 52 + 82 + 442 = 452 82 + 122 + 512 = 532 42 + 92 + 482 = 492 272 + 282 + 362 = 532 32 + 102 + 542 = 552 72 + 82 + 562 = 572 62 + 142 + 572 = 592 62 + 92 + 582 = 592 52 + 102 + 622 = 632 122 + 152 + 602 = 632 82 + 92 + 722 = 732 332 + 442 + 482 = 732 72 + 102 + 742 = 752 102 + 142 + 732 = 752 62 + 112 + 782 = 792 52 + 122 + 842 = 852 92 + 102 + 902 = 912 72 + 122 + 962 = 972 162 + 632 + 722 = 972 252 + 602 + 722 = 972
Omhoog
Pythagoras meerdimensionaal
De 'diagonaal' van een 4-hyperbalk De 'diagonaal' van een 5-hyperbalk 32 + 42 + 122 + 842 = 852 32 + 42 + 122 + 842 + 1322 = 1572
Omhoog
Kwadratische stambreuken
Kwadratische stambreuken zijn bruikbaar bij parallel geschakelde impedanties.
Als a2 + b2 = c2 is, is 1/(acn)2 + 1/(bcn)2 = 1/(abn)2 met n als positief geheel getal.
a b c 1/(ac)2 + 1/(bc)2 = 1/(ab)2 3 4 5 <1/152 + 1/202 = 1/122/td> 5 12 13 1/652 + 1/1562 = 1/602 8 15 17 1/1362 + 1/2552 = 1/1202 7 24 25 1/1752 + 1/6002 = 1/1682 20 21 29 1/5802 + 1/6092 = 1/4202 12 35 37 1/4442 + 1/12952 = 1/4202 28 45 53 1/14842 + 1/23852 = 1/12602 48 55 73 1/35042 + 1/40152 = 1/26402 16 63 65 1/10402 + 1/40952 = 1/10082 9 40 41 1/3692 + 1/16402 = 1/3602 33 56 65 1/21452 + 1/36402 = 1/18482 65 72 97 1/63052 + 1/69842 = 1/46802 11 60 61 1/6712 + 1/36602 = 1/6602 39 80 89 1/34712 + 1/71202 = 1/31202
Omhoog
De oppervlakte van driehoeken
De oppervlakte van een driehoek met zijden a, b en c is O = A(a , b , c)
De oppervlakte van driehoek met zijden ak, bk en ck is dan k2O
a b c opp a b c opp 6 5 5 12 8 5 5 12 4 13 15 24 3 25 26 36 7 15 20 42 9 10 17 36 6 25 29 60 10 13 13 60 13 13 24 60 11 13 20 66 5 29 30 72 8 29 35 84 10 17 21 84 13 14 15 84 12 17 25 90 16 17 17 120 19 20 37 114 17 17 30 120 16 25 39 120 15 28 41 126 13 20 21 126 11 25 30 132 15 26 37 156 10 35 39 168 14 25 25 168 25 25 48 168 13 30 37 180 17 25 26 204 17 25 28 210 17 28 39 210 12 39 45 216 13 37 40 240 13 40 45 252 15 34 35 252 15 37 44 264 17 39 44 330 17 40 41 336 18 41 41 360 25 29 36 360 24 37 37 420 25 34 39 420 29 29 40 420 29 29 42 420 29 35 48 504
Omhoog
Zes ribben en vier oppervlakken
van een driezijdige piramide
6 ribben 4 oppervlakken a b c d e f abf ace bcd def 24 20 13 11 13 20 192 60 6 66 24 15 7 20 25 15 108 84 42 150 24 20 7 15 25 20 192 84 42 150 28 26 25 17 17 30 336 210 204 120 37 24 13 13 40 37 420 240 60 240 30 25 16 39 34 25 300 240 120 420 34 25 16 39 30 39 420 240 120 540 45 24 13 13 40 51 540 252 60 156 30 29 27 52 51 5 72 324 270 126 39 33 25 52 16 60 594 120 330 384 34 33 25 52 39 65 264 420 330 1014 44 39 33 60 55 17 330 726 594 462 39 34 33 65 60 25 420 594 264 750 39 33 25 52 56 60 594 420 330 1344
Omhoog
Willekeurig viervlak;
drie verschillende oppervlakkenDrie verschillende oppervlakken a b c d e f abf ace bcd def 17 16 10 10 9 17 120 36 48 36 24 15 13 4 13 15 108 60 24 24 24 15 13 14 13 15 108 60 84 84 24 20 15 7 15 20 192 108 42 42 24 20 13 21 13 20 192 60 126 126 24 20 15 25 15 20 192 108 150 150 30 25 17 12 17 25 300 120 90 90 30 25 17 26 17 25 300 120 204 204 48 26 25 3 25 26 240 168 36 36 37 24 13 13 30 37 420 180 60 180 37 24 15 15 26 37 420 156 108 156 40 29 25 6 25 29 420 300 60 60 37 24 20 20 19 37 420 114 192 114 41 18 15 15 28 41 360 126 108 126 48 30 25 11 25 30 432 168 132 132 37 24 15 15 44 37 420 264 108 264 42 35 29 8 29 35 588 420 84 84 41 18 15 15 52 41 360 234 108 234 48 30 25 25 25 30 432 168 300 300 40 29 25 36 25 29 420 300 360 360 37 24 20 20 51 37 420 306 192 306 48 26 25 17 25 26 240 168 204 204 39 30 17 17 28 39 540 210 120 210 39 30 17 17 44 39 540 330 120 330 39 30 25 25 40 39 540 468 300 468 48 40 25 25 25 40 768 168 300 300 39 30 25 25 56 39 540 420 300 420 48 40 25 39 25 40 768 168 468 468 42 35 29 48 29 35 588 420 504 504 39 30 25 25 34 39 540 420 300 420
Omhoog
Willekeurig viervlak; twee verschillende oppervlakken
Twee verschillende oppervlakken a b c d e f abf ace bcd def 15 13 4 15 13 14 84 24 24 84 17 10 9 17 10 21 84 6 36 84 20 13 11 20 13 21 98 126 66 66 126 20 15 7 20 15 25 150 42 42 150 25 20 15 7 20 15 150 150 42 42 25 17 12 25 17 26 204 90 90 204 26 25 3 26 25 17 204 36 36 204 25 17 12 25 17 28 210 90 90 210 29 21 20 13 21 20 210 210 126 126 25 17 16 17 39 28 210 120 120 210
Omhoog
Willekeurig viervlak; gelijke oppervlakken
Vier gelijke oppervlakken a b c d e f abf ace bcd def 28 25 17 28 39 17 210 210 210 210 26 25 17 26 25 17 204 204 204 204 39 34 25 39 56 25 420 420 420 420
De figuur hieronder vertoont twee vierkanten:
Omhoog Wiskunde Hoofdmenu